Lịch Sử Của Diện Tích Xung Quanh Hình Nón

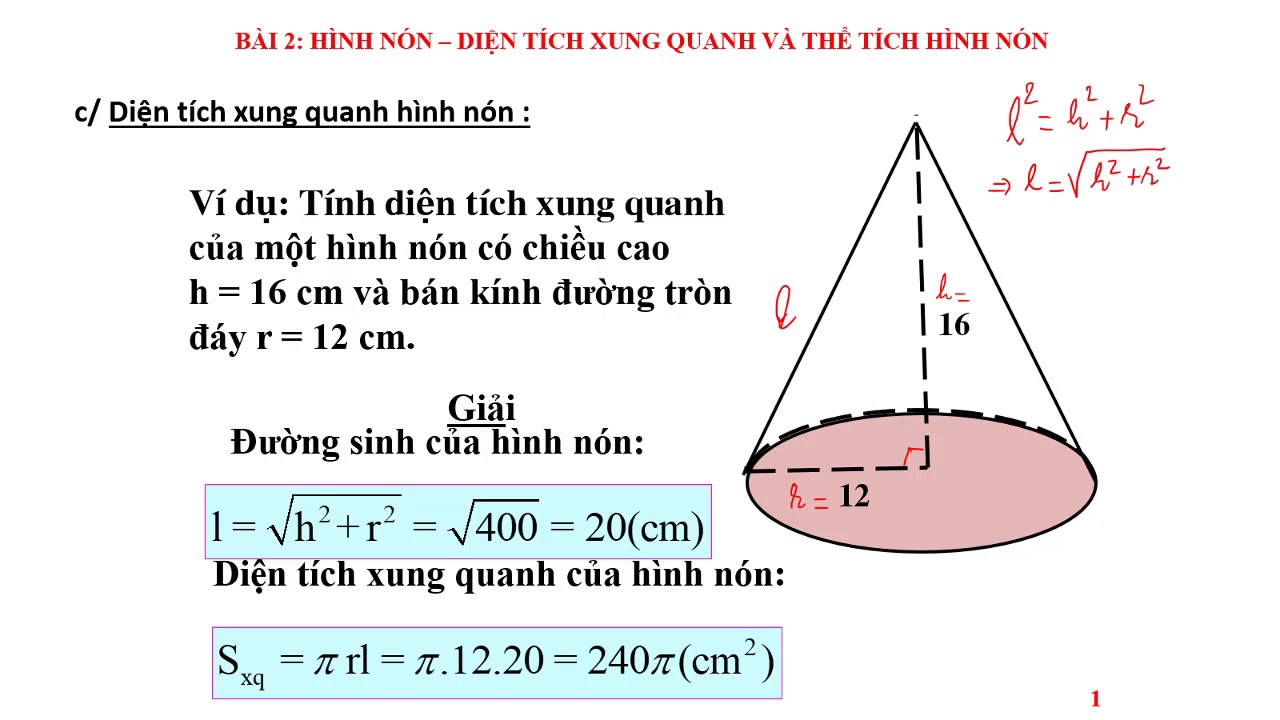
Diện tích xung quanh hình nón

1. Các bước vẽ hình nón:

Để vẽ hình nón, bạn có thể làm theo các bước sau:
Bước 1: Vẽ hình tròn đáy
Bắt đầu bằng việc vẽ một hình tròn. Hình tròn này sẽ là đáy của hình nón. Để tạo cảm giác ba chiều, hãy vẽ hình tròn này thành một hình elip nhẹ (đối với hình nón đặt nghiêng).
Bước 2: Xác định đỉnh nón
Xác định đỉnh của hình nón, đây sẽ là điểm cao nhất và nằm ở phía trên hình elip vừa vẽ. Đỉnh này sẽ là nơi tất cả các cạnh của nón hội tụ.
Bước 3: Vẽ các cạnh bên của hình nón

Hình nón cụt

Kết nối đỉnh nón với hai điểm đối diện trên hình elip bằng hai đoạn thẳng. Đây sẽ là các cạnh bên của hình nón.
Bước 4: Hoàn thiện đáy nón
Nếu bạn đang vẽ hình nón nghiêng, hãy vẽ một phần của hình elip đáy phía sau để tạo cảm giác về độ sâu. Phần này thường bị che khuất và chỉ vẽ một nửa của elip.
Bước 5: Tạo bóng và chi tiết
Để tạo hiệu ứng ba chiều, hãy thêm bóng ở một bên của hình nón để làm nổi bật khối lượng và hình dạng. Vùng đối diện với nguồn sáng sẽ sáng hơn, còn vùng xa nguồn sáng hơn sẽ tối lại.
Mẹo bổ sung:
Sử dụng thước kẻ để đảm bảo các đường thẳng đều và sắc nét.
Có thể vẽ trước một hình tam giác cân để định hình cơ bản, sau đó thêm hình elip làm đáy và điều chỉnh các đường cong sao cho hợp lý.
Hình nón cơ bản sẽ có hình dạng rõ ràng và góc cạnh sắc nét khi hoàn thành

2. Áp dụng diện tích xung quanh hình nón trong công việc:

Các ứng dụng diện tích xung quanh của hình nón:

Trong thiết kế và sản xuất:

Thiết kế nón: Trong công nghiệp may mặc hoặc sản xuất đồ bảo hộ (nón bảo hiểm, nón thời trang), diện tích xung quanh giúp tính toán lượng vật liệu cần dùng để tạo ra một chiếc nón có kích thước mong muốn.
Vật liệu phủ: Trong sản xuất các sản phẩm hình nón (chẳng hạn như phễu, nắp hình nón, lều, hoặc tháp nhọn), diện tích xung quanh giúp xác định lượng vật liệu phủ bên ngoài, chẳng hạn như vải, kim loại, hoặc giấy.

Trong xây dựng:

Kiến trúc: Khi thiết kế các công trình kiến trúc có phần mái vòm hình nón (ví dụ: tháp chuông, tháp pháo), diện tích xung quanh hình nón có thể được dùng để tính toán lượng vật liệu như ngói hoặc kim loại cần thiết để phủ toàn bộ bề mặt bên ngoài.
Trang trí: Diện tích xung quanh cũng được sử dụng để tính toán chi phí và khối lượng vật liệu trang trí cho các công trình có kết cấu dạng hình nón.

Trong kỹ thuật và cơ khí:

Sản xuất phễu: Các thiết bị như phễu hình nón được sử dụng trong các ngành công nghiệp, từ chế biến thực phẩm đến xây dựng. Diện tích xung quanh của phễu giúp xác định bề mặt tiếp xúc hoặc lượng vật liệu cần thiết để chế tạo.
Tính toán diện tích sơn, phủ: Khi cần sơn hoặc phủ lớp bảo vệ cho các bề mặt hình nón, diện tích xung quanh cho phép ước lượng khối lượng sơn, chất phủ một cách chính xác, tránh lãng phí vật liệu.

Ứng dụng hình nón trong đời sống

Trong giáo dục và nghiên cứu:

Bài toán thực tế: Trong dạy học hoặc nghiên cứu khoa học, việc tính toán diện tích xung quanh của hình nón giúp minh họa các bài toán thực tế liên quan đến hình học không gian.
Ứng dụng mô hình: Diện tích xung quanh của hình nón được sử dụng trong các mô hình toán học và vật lý để mô phỏng các tình huống thực tế, ví dụ như dòng chất lỏng qua phễu hoặc lực phân bố trên một bề mặt hình nón.

Trong marketing và quảng cáo:

Thiết kế các bảng quảng cáo: Các thiết kế bảng, biểu tượng, hoặc mô hình quảng cáo có dạng hình nón, như các bảng đứng hoặc mô hình quảng bá sản phẩm, có thể yêu cầu tính toán diện tích xung quanh để thiết kế và tạo ra mô hình một cách chính xác.
Kết luận:
Việc áp dụng diện tích xung quanh của hình nón vào công việc giúp bạn tính toán chính xác lượng vật liệu, chi phí sản xuất, và các yêu cầu kỹ thuật liên quan, giúp tối ưu hóa quy trình và tăng hiệu quả trong nhiều lĩnh vực khác nhau.

3. Người phát minh ra diện tích xung quanh hình nón:

Khái niệm diện tích xung quanh của hình nón đã được phát triển qua nhiều thế kỷ bởi nhiều nhà toán học và nhà khoa học. Tuy nhiên, một số nhân vật nổi bật có ảnh hưởng lớn trong việc phát triển các lý thuyết hình học cơ bản, bao gồm cả diện tích xung quanh của hình nón, là:
Euclid (khoảng 300 TCN): Một trong những nhà toán học vĩ đại của Hy Lạp cổ đại, Euclid đã viết "Elementa" (Các yếu tố), một trong những tài liệu hình học có ảnh hưởng nhất. Trong công trình của mình, ông đã trình bày các định lý về hình học mà sau này là nền tảng để phát triển các công thức tính toán diện tích và thể tích của các hình dạng như hình nón.

Archimedes - nhà hình học vĩ đại

Archimedes (khoảng 287–212 TCN): Archimedes là một nhà toán học và nhà vật lý nổi tiếng, và ông đã đóng góp lớn cho sự hiểu biết về hình học không gian. Mặc dù ông không trực tiếp phát minh ra công thức diện tích xung quanh của hình nón, nhưng các nghiên cứu của ông về thể tích và diện tích bề mặt của các hình dạng 3D đã đặt nền tảng cho các công thức sau này.
Isaac Newton (1643–1727) và Gottfried Wilhelm Leibniz (1646–1716): Hai nhà toán học này đồng thời phát triển phép tính tích phân, một công cụ quan trọng trong việc tính toán các diện tích và thể tích của các hình dạng phức tạp. Công thức tính diện tích xung quanh của hình nón có thể được suy ra từ các nguyên lý cơ bản của phép tính tích phân mà họ đã phát triển.
Tóm lại
Diện tích xung quanh của hình nón không phải là phát minh của một cá nhân cụ thể mà là kết quả của sự phát triển và tích lũy kiến thức trong lĩnh vực hình học và toán học qua nhiều thế kỷ. Các nhà toán học cổ đại như Euclid và Archimedes đã đặt nền tảng, trong khi các nhà toán học hiện đại như Newton và Leibniz đã phát triển các công cụ toán học cần thiết để tính toán diện tích và thể tích của các hình dạng không gian.

4. Tìm hiểu về cấu trúc hình nón:

Hình nón là một hình dạng 3D rất phổ biến trong hình học và có ứng dụng rộng rãi trong đời sống và khoa học. Dưới đây là một cái nhìn chi tiết về cấu trúc của hình nón:
Cấu trúc của Hình Nón
Đáy (Base):
Hình dạng: Đáy của hình nón là một hình tròn (hoặc hình elip trong trường hợp nón nghiêng hoặc không đều).
Bán kính (r): Là khoảng cách từ tâm của đáy đến bất kỳ điểm nào trên viền đáy. Đối với đáy hình tròn, bán kính là hằng số, trong khi đối với đáy hình elip, bán kính là hai trục bán kính của elip.
Đỉnh (Apex):
Vị trí: Đỉnh là điểm duy nhất trên đỉnh của hình nón và không nằm trên mặt đáy. Đây là điểm nơi tất cả các đường sinh của nón gặp nhau.
Khoảng cách từ đỉnh đến đáy: Được gọi là chiều cao (h) của hình nón.
Đường sinh (Slant Height, l):
Định nghĩa: Đường sinh là khoảng cách từ đỉnh của hình nón đến một điểm bất kỳ trên viền của đáy.
Tính toán: Được tính bằng định lý Pythagoras trong tam giác vuông hình nón, khi bạn biết chiều cao và bán kính của đáy: 
Các Cạnh bên (Generatrices):
Định nghĩa: Cạnh bên là các đoạn thẳng nối từ đỉnh đến các điểm trên viền đáy, tạo thành mặt bên của hình nón.
Mặt bên (Lateral Surface):
Định nghĩa: Mặt bên của hình nón là bề mặt cong nối từ đáy đến đỉnh. Nó có thể được tưởng tượng như một hình nón được cắt mở và trải ra thành một hình quạt trong mặt phẳng.
Công thức liên quan
Diện tích xung quanh (Lateral Surface Area):
Bao gồm diện tích xung quanh cộng với diện tích đáy.
Hình học và Toán học
Hình học: Hình nón là một trong những hình dạng cơ bản trong hình học không gian. Nó được sử dụng để giải quyết các bài toán về diện tích và thể tích trong nhiều tình huống thực tế.
Toán học ứng dụng: Công thức tính toán cho hình nón có ứng dụng trong nhiều lĩnh vực như thiết kế kỹ thuật, kiến trúc, sản xuất và vật lý.
Ứng dụng thực tiễn
Kiến trúc và Xây dựng: Mái nhà hình nón, tháp chuông, hoặc các cấu trúc giống như nón.
Sản xuất: Phễu công nghiệp, nón bảo hiểm, và các bộ phận máy móc có dạng hình nón.
Khoa học và Kỹ thuật: Các mô hình toán học và mô phỏng trong các bài toán kỹ thuật.
Tóm lại
Hình nón là một cấu trúc hình học đơn giản nhưng rất quan trọng với nhiều ứng dụng trong thực tế. Việc hiểu rõ cấu trúc của nó giúp giải quyết các bài toán về diện tích và thể tích, cũng như thiết kế và sản xuất các sản phẩm có dạng hình nón.